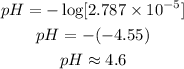Question

A common acid in energy drinks is phosphoric acid .a) What is the molarity of a solution containing 0.0000209 mol acid in 750 mL of solution? b) What is the pH of the acid in the drink?

Answer 1

Explanations:

a) The formula for calculating the molarity of a solution is expressed according to the formula shown below:

`\text{Molarity}=\frac{Moles\text{ of solute}}{Litres\text{ of solution}}`

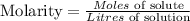
Given the following parameters;

Moles of the solution = 0.0000209 mol

Volume of solution = 750mL

Convert the volume to litres

`\begin{gathered} V_s=750mL*(1l)/(1000mL) \\ _{}V_s=(750L)/(1000) \\ V_s=0.750L \end{gathered}`

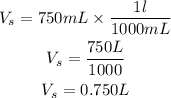
Get the required molarity using the formula above;

`\begin{gathered} \text{Molarity}=(0.0000209)/(0.750) \\ \text{Molarity}=2.787*10^(-5)M \end{gathered}`

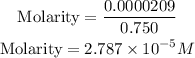
b) To get the pH of the acid in the drink, we will use the formula;

`\begin{gathered} pH=-\log \lbrack H^+(aq)\rbrack \\ \end{gathered}`

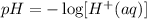
The expression in the square bracket is the molarity of the solution. Substituting the given molarity into the formula:

`\begin{gathered} pH=-\log \lbrack2.787*10^(-5)\rbrack \\ pH=-(-4.55) \\ pH\approx4.6 \end{gathered}`