12a)
Since there are 2/3 of multigrain bagels of 12 bagels, we can apply the rule of three:
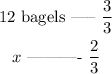
where x denote the multigrain bagels. Then, x is given by
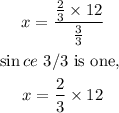
Then, we have
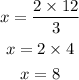
and the answer is 8 multigrain bagels.
12b)
Similarly, we can apply the rule of three as
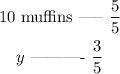
where y denotes the bran muffins. Then y is given by
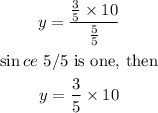
So, we have
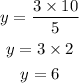
and the answer is 6 bran muffins.