Question

Date 31 Properties of Parubolas Identify the vertex of each + 10x 164 You 128 164 wordinate 2) y-2-4-2 yvquestion 4 please

Answer 1

Since the equation of the parabola is in its standard form then you can first find the x coordinate of the vertex like this:

`\begin{gathered} (-b)/(2a)\Rightarrow\text{ x-coordinate} \\ \text{ Where} \\ y=ax^2+bx+c\Rightarrow\text{ standard form} \end{gathered}`

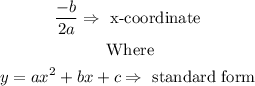
In this case, you have

`\begin{gathered} y=-3x^2+12x-10 \\ a=-3 \\ b=12 \\ c=-10 \end{gathered}`
`(-b)/(2a)=(-12)/(2(-3))=(-12)/(-6)=2\Rightarrow\text{ x-coordinate}`

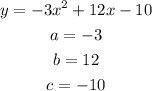
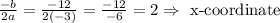
Now, replace this value into the equation of the parabola to find the y-coordinate of the vertex:

`\begin{gathered} y=-3x^2+12x-10 \\ x=2 \\ y=-3(2)^2+12(2)-10 \\ y=-3(4)+24-10 \\ y=-12+14 \\ y=2 \end{gathered}`

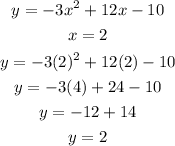
Therefore, the vertex of the parabola is (2,2).