Question

3.) A prism with a volume of 270 m³ is dilated by a factor of 3.What is the volume of the dilated prism?4.) A prism with a base area of 8 cm² and a height of 6 cm is dilated by a factor of 54.What is the volume of the dilated prism?5.) A prism with a volume of 3125 ft³ is scaled down to a volume of 200 ft³.What is the scale factor?

Answer 1

3) In general, a dilation is an enlargement of the sides of a shape, even if it is a 3D shape.

Furthermore, the volume of a prism is given by the formula

`V=A_{\text{base}}\cdot h=l\cdot w\cdot h`

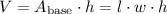
Then,

`V_{\text{new}}=3l\cdot3w\cdot3w=3^3(l\cdot w\cdot h)=27V_(initial)`

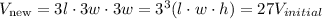
Therefore,

`\Rightarrow V_{\text{new}}=27\cdot(270)=7290`

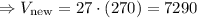
The answer to part 3) is 7290 m^3

4) Due to similar reasoning, in general, the area of a shape is given by

`A=l\cdot w`

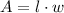
If we apply a dilation to that area,

`\Rightarrow A_{\text{new}}=kl\cdot kw=k^2A_(original)`

Where k is the dilation factor.

Thus, in our case,

`\begin{gathered} \Rightarrow A_{\text{new}}=(54)^2\cdot8=23328 \\ \text{and} \\ h_{\text{new}}=54\cdot6=324 \end{gathered}`

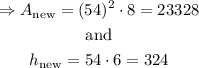
Therefore,

`\Rightarrow V_{\text{new}}=A_{\text{new}}\cdot h_{\text{new}}=23328\cdot324=7558272`

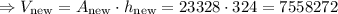
The answer to part 4) is 7558272 cm^3

5) From the answer to question 3)

`V_{\text{new}}=k^3\cdot V_(original)_{}`

Thus,

`\begin{gathered} \Rightarrow3125=k^3\cdot200 \\ \Rightarrow k^3=(3125)/(200)=(125)/(8) \\ \Rightarrow k=(5)/(2)=2.5 \\ \Rightarrow k=2.5 \end{gathered}`

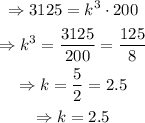
The answer to part 5) is 2.5