Question

Can you help me to solve the other half of this problem? I don’t know what I’m doing wrong

Answer 1

Let's start by copying the equation:

`-5\cos ^2(x)+4\cos (x)+1=0`

To make it easier to see, let's substitute cos(x) by "u":

`-5u^2+4u+1=0`

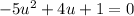
To find the values of "u", we can use Bhaskara's Equation:

`\begin{gathered} u=\frac{-4\pm\sqrt[]{4^2-4\cdot(-5)\cdot1}}{2\cdot(-5)} \\ u=\frac{-4\pm\sqrt[]{16+20}}{-10} \\ u=\frac{-4\pm\sqrt[]{36}}{-10} \\ u=(-4\pm6)/(-10) \end{gathered}`
`\begin{gathered} u_1=(-4+6)/(-10)=(2)/(-10)=-0.2 \\ u_2=(-4-6)/(-10)=(-10)/(-10)=1 \end{gathered}`

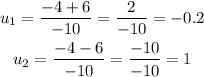
Now, let's substitute cos(x) back:

`\begin{gathered} \cos (x_1)=-0.2 \\ \cos (x_2)=1 \end{gathered}`

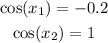
Since it is a trigonometric solution, we have repeating values of "x" that satisfy each equation above.

The first, the one you already got, comes from

`\begin{gathered} \cos (x)=1 \\ x=0+2\pi k \\ x=2\pi k \end{gathered}`

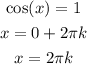
The smallest non negative is for k = 0 which gives

`x=0`

The next following this part would be for k = 1, which gives:

`x=2\pi`

However, we have another equation for solutions:

`\cos (x)=-0.2_{}`

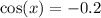
For this equation, the smallest "x" value can be found using arc-cossine of -0.2 in a calculator, which gives:

`\begin{gathered} x=\arccos (-0.2) \\ x=1.772\ldots \end{gathered}`

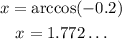
This is the next non-negative solution for the equation, because it is smaller than the other we found.

So the second part is x = 1.772.