Question

The percent of fat calories that a person in America consumes each day is normally distributed with a mean of about 36 and a standard deviation of 10. Suppose that one individual is randomly chosen. Let X= percent of fat calories.(a) Find the z-score corresponding to 30 percent of fat calories, rounded to 3 decimal places. (b) Find the probability that the percent of fat calories a person consumes is more than 30. (c) Find the maximum number for the lower quarter of percent of fat calories. Round your answer to 3 decimal places.

Answer 1

Write out the given parameters

`\begin{gathered} \mu=36 \\ \sigma=10 \\ x=30 \end{gathered}`

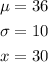
a). The Z-score is given by

`\begin{gathered} z=(x-\mu)/(\sigma) \\ z=(30-36)/(10) \\ \end{gathered}`

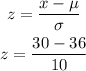
Then

`z=-(6)/(10)=-0.600`

Hence

The Z-score value corresponding to 30 % of fat calories is -0.600

b). The probability that the percent of fat calories a person consumes is more than 30 is given by

`p(x>30)=p(z>-0.6)=0.7257469`

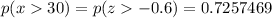
Hence

The probability that the percent of fat calories a person consumes is more than 30 is 0.7257