The acceleration of the car can be given as,
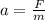
Plug in the known values,
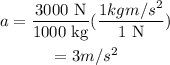
The net force which acts on the car is,
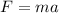
The frictional force acting on the car is,
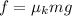
The net force is balanced by the frictional force which can be solved as,
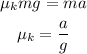
Substitute the known values,
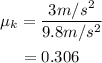
Thus, the coefficient of kinetic friction is 0.306.