Question

given the following exponential function, identify whether the change represents growth or decay, and determine the percentage rate of increase or decrease. y=590(1.061)^x

Answer 1

Given the exponential function:

`y=590(1.061)^x`

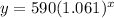
Let's determine if the exponential function represents growth or decay.

Take the exponential function:

`y=a(b)^x`

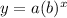
Where b is the base.

• If the base of an exponential function is greater than one, the exponential function represents growth

• If the base of an exponential function is between 0 and 1, the function represents a decay function.

Here, the base of the exponential function, b is 1.061 which is greater than 1, the function represents a growth function.

SInce it is represents a growth function, let's determine the percentage rate of increase.

The general formula for exponential growth is:

`y=a(1+r)^x`

Where r is the growth rate.

Thus, we have:

`\begin{gathered} y=590(1+(1-1.061)^x \\ \\ y=590(1+0.061)^x \end{gathered}`

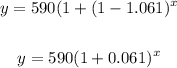
The growth rate, r is = 0.061

The percentage rate of increase is:

`\text{percentage rate of increase = }0.061\ast100=6.1\text{\%}`

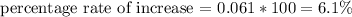
Therefore, the percentage rate of increase is 6.1%

ANSWER:

The function represents growth

Percentage rate of increase = 6.1%