Question

The Garcia family has two cars. Last week, the first car consumed 35 gallons ofgas and the second consumed 25 gallons of gas. The two cars drove acombined total of 1,025 miles, and the sum of their fuel efficiencies was 35miles per gallon. What was the fuel efficiency of each of the cars last week?First car: 15 miles per gallonSecond car: 20 miles per gallonFirst car: 10 miles per gallonSecond car: 25 miles per gallonFirst car: 20 miles per gallonSecond car: 15 miles per gallonFirst car: 25 miles per gallonSecond car: 10 miles per gallon

Answer 1

Let x be the efficiency for the first car and let y be the efficiency for the second car.

We know that the firt car consumed 35 gallons, the second 25 gallons and that they drove a combined total of 1025 miles, then we have the equation:

`35x+25y=1025`

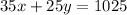
We also know that the sum of their efficiencies was 35, then we have:

`x+y=35`

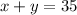
Hence we have the system of equations:

`\begin{gathered} 35x+25y=1025 \\ x+y=35 \end{gathered}`

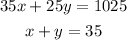
To find the solution of the system let's solve the second equation for y:

`y=35-x`

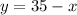
Plugging this in the first equation we have:

`\begin{gathered} 35x+25(35-x)=1025 \\ 35x+875-25x=1025 \\ 10x=1025-875 \\ 10x=150 \\ x=(150)/(10) \\ x=15 \end{gathered}`

Now that we have the value of x we plug it in the expression for y:

`\begin{gathered} y=35-15 \\ y=20 \end{gathered}`

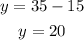
Therefore the efficiency of the first car was 15 miles per gallon and the efficiency of the second car was 20 miles per gallon