Please help me with this sample question.The sample questions only allow me to test each country once before moving to the next. I need all countries.

Question

asked Aug 3, 2023 45.0k views

2 Answers

Mrjmh · Answer 1 · 2023-08-07T04:13:59+0000

Let be "a" the number of medals that Country A won, "b" the number of medals that Country B won, and "c" the number of medals that Country C won.

You can set up the following System of equations using the information given in the exercise:

$\begin{cases}a+b+c=119 \\ b=c+7 \\ a=b+c+33\end{cases}$

In order to solve the System of equations, you can follow these steps:

1. Substitute the second equation into the third equation:

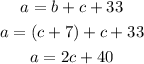
$\begin{gathered} a=b+c+33 \\ a=(c+7)+c+33 \\ a=2c+40 \end{gathered}$

2. Substitute this new equation and the second original equation, into the first original equation:

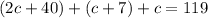
3. Solve for "c":

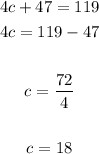
$\begin{gathered} 4c+47=119 \\ 4c=119-47 \\ \\ c=(72)/(4) \\ \\ c=18 \end{gathered}$

4. Knowing the value of "c", you can substitute it into the second original equation and then evaluate, in order to find the value of "b":

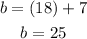
$\begin{gathered} b=(18)+7 \\ b=25 \end{gathered}$

5. Knowing the value of "b" and "c", you can substitute them into the third original equation and then evaluate, in order to find the value of "a":

$\begin{gathered} a=b+c+33 \\ a=(25)+(18)+33 \\ a=76 \end{gathered}$

Therefore, the answer is:

- Country A won 76 medals.

- Country B won 25 medals.

- Country C won 18 medals.