We can divide the hexagon into 6 equilateral triangles, and call the side 'x'. I will draw the situation:
Every line is x because the hexagon is regular (all sides have the same length). Therefore we can find x, because two times x is 18'':
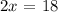
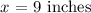
The hexagon has the same area of 6 equilateral triangles with the side equal to x. The formula of the area of an equilateral triangle is:
![Area\text{ = }\frac{x^2\sqrt[]{3}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/o8jjo5p3c3o4wjeqphnkjd7ftnkem0vrnn.png)
Therefore the area of the hexagon will be:
![\text{AreaHexagon = 6}*\frac{x^2\sqrt[]{3}}{4}^{}](https://img.qammunity.org/2023/formulas/mathematics/college/h60taaiyb9yedh8zfti7onk0n8iplnym4a.png)
![\text{AreaHexagon = 6}*\frac{9^2\sqrt[]{3}}{4}^{}](https://img.qammunity.org/2023/formulas/mathematics/college/4ixcmz8py0d1h0sru13cmi38w19h6rxwfl.png)
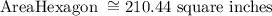
Rounding it will be 210 square inches.