Since the lizard increases by about 8% each year, it can be understood as an exponential function as:

since the initial length and the rate of increase is also given, replace ins the formula
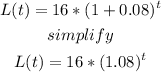
Then replace in the formula t as 3
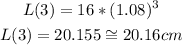
Answer:
The equation that models the length of the lizard for the first 8 years is:
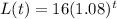
And the approximate length of the lizard after 3 years is about 20.16 cm