the equation given
we can rewrite the equation as
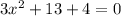
to solve this question, we can use any of the given mehod known to solve quadratic equations which are
1. factorization
2. completing the squares
3. using quadratic equation
for the purpose of this tutoring session, i'll use quadratic equation also know as quadractic formula
the formula is given as
![x=-b\pm\frac{\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/yxah1hw3iilwvjgis2v5jk7g8mxz8s2a12.png)
next we proceed to identify the variables
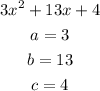
now we can input the values into the equation (formula) above
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-13\pm\sqrt[]{13^2-4(3)(4)}}{2(3)} \\ x=\frac{-13\pm\sqrt[]{169-48}}{6} \\ x=\frac{-13\pm\sqrt[]{121}}{6} \\ x=(-13\pm11)/(6) \\ x=-(13+11)/(6) \\ or \\ x=-(13-11)/(6) \\ x=-(2)/(6) \\ or \\ x=-(24)/(6) \\ x=-(1)/(3) \\ or \\ x=-4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qzczvc7qgtiwjld3ow90v5t1macrddoymo.png)
from the calculations above, x = -1/3 or x = -4