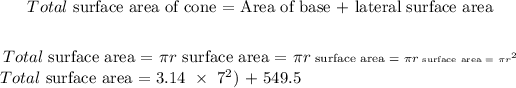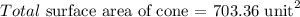Question

Calculate the cone: 1) volume; 2) the area of the lateral surface; 3) the total surface area;for AB = 14, SO = 24.

Answer 1

Answer:
`\begin{gathered} a)\text{ Volume = 1230.88 units}^3 \\ b)\text{ lateral ssurface = 549.5 units}^2\text{ } \\ c)\text{ }Total\text{ surface area of cone = 703.36 unit}^2 \end{gathered}`Step-by-step explanation:

Given:

AB = 14

SO = 24

To find:

a) the volume

b) the area of the lateral surface

c) the total surface area

a) To find the volume of the cone, we will use the formula:

`Volume\text{ of a cone = }(1)/(3)πr²h`

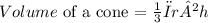
r = radius

diameter = AB = 14

diameter = 2(radius)

radius = diameter/2 = 14/2

radius = 7

height = SO = 24

let π= 3.14

`\begin{gathered} Volume\text{ of the cone = }(1)/(3)*3.14*7^2*24 \\ Volume\text{ of the cone = 1230.88 unit}^3 \end{gathered}`

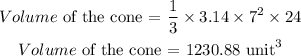
b) To get the lateral surface, we will apply the formula:

`\begin{gathered} Lateral\text{ surface of the cone = 3.14 }*7*√(7^2+24^2) \\ \\ Lateral\text{ surface area of the cone = 549.5 units}^2 \end{gathered}`

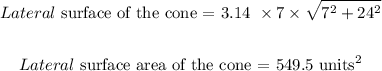
c) The total surface area formula:

`\begin{gathered} Total\text{ surface area of cone = Area of base + lateral surface area} \\ \\ Total\text{ surface area = \pi r}^2\text{ + \pi rl} \\ \\ Total\text{ surface area = \lparen3.14 }*\text{ 7}^2)\text{ + 549.5} \end{gathered}`
`Total\text{ surface area of cone = 703.36 unit}^2`