Question

find the present value for the following future amount $9780 at 2.5% compounded semiannually for 11 years (do not round until the final answer. then round to the nearest cent as needed)

Answer 1

The compound interest formula is given by:

`A=P(1+(r)/(n))^(nt)`

where P is the principal (the initial value), r is the interest rate in decimal form, n is the number of times the interest is compounded in a given time t.

In this case we know that the future amount is 9780, this means that A=9780. Furthermore, we know that r=0.025, n=2 (since the interest is compounded semiannually) and t=11. Pluging this values in the formula a solving for P, we have:

`\begin{gathered} 9780=P(1+(0.025)/(2))^(2\cdot11) \\ P=(9780)/((1+(0.025)/(2))^(2\cdot11)) \\ P=7441.29 \end{gathered}`

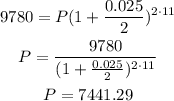
Therefore, the present value of our investment is $7441.29.