To solve this, let's think about what are the numbers that are at a distance of 1 from 8. We can take 8 and:

Those are the only two numbers that verify the asked. Now we need to express it using absolute value notation. If two numbers are at a certain 'distance', this means that their difference is that 'distance'. Since we want the distance between a number x and 8 to be 1, we can write:
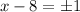
Because:
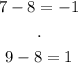
And we can write this plus-minus sign using absolute value:

Thus, the answer is:
