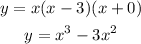Answer:
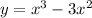
Explanation:
Given that on x=0 y=0, and x=3 y=0 the function has roots.
We can state that the function can be considered as:
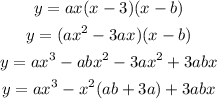
By the given table:
We can use two of the points given and create a system of 2 equations with two variables, and solve it for a and b:
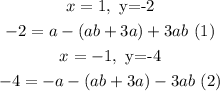
Then, we can divide both equations to find b.
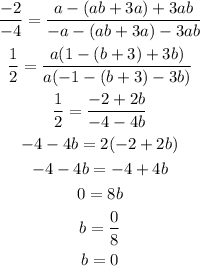
Now, knowing the value of b, we can substitute it into either equation and find a, to get the cubic function that models the data:

Hence, the function that satisfies the data would be: