Question

Mary takes sightseeing tour that can fly 450 miles at 35mph headwind in the same amount of time it can travel 702 miles with 35mph. Find the speed of the helicopter Number 429

Answer 1

Given:

The distance traveled by helicopter against the headwind, d₁=450 miles

The speed of the wind, w=35 mph

The distance traveled by helicopter the tailwind, d₂=702 miles

To find:

The speed of the helicopter.

Step-by-step explanation:

Let us assume that the time it takes for the helicopter to travel the distances is t

The time duration for an object to cover a distance is given by,

`T=(d)/(u)`

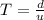
Where t is the time, d is the distance, and u is the velocity.

As the time it takes for the helicopter to cover the distances d₁ and d₂ are the same,

`(d_1)/(v-w)=(d_2)/(v+w)`

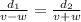
Where v-w is the total speed of the helicopter when it is flying against the headwind and v+w is the speed of the helicopter when it is flying with a tailwind.

On substituting the known values,

`\begin{gathered} (450)/(v-35)=(702)/(v+35) \\ \implies450v+15750=702v-24570 \\ 15750+24570=(702-450)v \\ \implies v=(40320)/(252) \\ =160\text{ m/s} \end{gathered}`

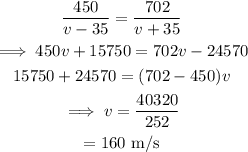
Final answer:

Thus the speed of the helicopter is 160 m/s