Question

The second and third terms of a geometric series are 128 and 96 respectively. Find the first term.170.6796128256

Answer 1

Given: The second and third terms of a geometric series are 128 and 96 respectively.

Required: The first term.

Step-by-step explanation:

Let the first term of the Geometric Series is 'a' and common ration is 'r'.

Given that second term is 128 and third term is 96.

So

`\begin{gathered} ar=128 \\ ar^2=96 \end{gathered}`

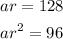
Dividing both, we get

`\begin{gathered} (ar)/(ar^2)=(128)/(96) \\ r=(3)/(4) \end{gathered}`

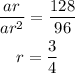
Put this in 1st

`\begin{gathered} a((3)/(4))=128 \\ a=(128*4)/(3) \end{gathered}`

Thus

`a=(512)/(3)=170.67`

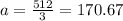
Hence, first term is 170.67

Final Anwer: Option 1 is correct answer.