Question

Please solve the problem step by step, to check my final answers.

Answer 1

We are asked to determine the future value and the time for a quarterly compounded interest. To do that we will use the following formula:

`A=P(1+(r)/(400))^(4t)`

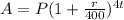
Where:

`\begin{gathered} A=\text{ future value} \\ P=\text{ initial value} \\ r=\text{ interest rate} \\ t=\text{ time} \end{gathered}`

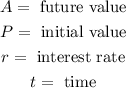
Part A. We are asked to determine the time in 7 years. To do that we will substitute the value of "t = 7" and "r = 2", we get:

`A=4000(1+(2)/(400))^((4)(7))`

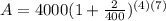
Solving the operations:

`A=4599.49`

Therefore, in 7 years there will be the amount of $4599.49

Part B. We are asked to determine the time to get the amount of $5000. To do that we will substitute the value of "A = 5000", and we get:

`5000=4000(1+(2)/(400))^(4t)`

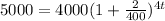
Now, we solve for "t". First, we divide both sides by 4000:

`(5000)/(4000)=(1+(2)/(400))^(4t)`

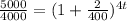
Now, we take the natural logarithm to both sides:

`\ln((5000)/(4000))=\ln(1+(2)/(400))^(4t)`

Now, we use the following property of logarithms:

`\ln x^y=y\ln x`

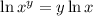
Applying the property we get:

Now, we divide both sides by the natural logarithm and by 4:

`(1)/(4)(\ln((5000)/(4000)))/(\ln(1+(2)/(400)))=t`

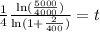
Solving the operations:

`11.19=t`

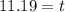
Therefore, the amount of 5000 will be obtained after 11.19 years.