Question

Find the distance between (14,-6) and (12,8)

Answer 1

For explanation purposes I'll call Point A (14,-6) and Point B (12,8) the given points.

To calculate the distance between both points you have to calculate the distance between each coordinate over the x and y axis.

Then apply the Phytagoras theorem to calculate its length.

I'll sketch the points:

x-axis

`base=d_(AB)=x_A-x_B=14-12=2`

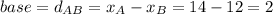
y-axis

`heigth=d_(AB)=y_B-y_A=8-(-6)=8+6=14`

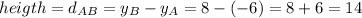
Now according to the Phythagoras theorem, the sum of the squared base and the squared heigth of a triangle is equal to the squared hypotenuse:

`a^2+b^2=c^2`

For this triangle:

`\begin{gathered} 2^2+14^2=c^2 \\ c^2=200 \\ c=\sqrt[]{200}=10\sqrt[]{2}=14.14 \end{gathered}`

The distance between both points is 14.14 units.