Answer:
We'll need to invest $18,527.39
Explanation:
Remember that the formula for the present value of money is:
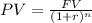
Where:
• PV, is the ,present value ,of money.
,
• FV, is the ,future value ,of money.
,
• r ,is the interest rate.
,
• n, is the times that the interest is compounded.
Now, we know that we're looking to get $25,000. This way,
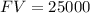
We're given an APR, but we know that our interest will compound monthly. Therefore, we have to convert the annual rate to monthly rate. We'll do so by dividing the annual percent rate by 12. This way, we'll have that:
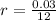
Since our interest compounds monthly, we'll have to find the number of months in 10 years. We'll do so by multiplying 10 by 12. This way,
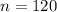
Using this data in the formula, as following:
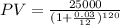
We'll have that:
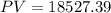
Therefore, we can conclude that we'll need to invest $18,527.39