we have the equation
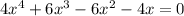

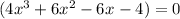
Note that
For x=1
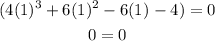
x=1 is a root of the given equation
so
Divide
(4x^3+6x^2-6x-4) : (x-1)
4x^2+10x+4
-4x^3+4x^2
---------------------------
10x^2-6x-4
-10x^2+10x
-----------------------
4x-4
-4x+4
-----------
0
therefore
(4x^3+6x^2-6x-4)=(x-1)(4x^2+10x+4)
Solve the quadratic equation
(4x^2+10x+4)=0
a=4
b=10
c=4
substitute in the formula
![x=\frac{-10\pm\sqrt[]{10^2-4(4)(4)}}{2(4)}](https://img.qammunity.org/2023/formulas/mathematics/college/uumo7lckqetib72usdvxd1zt9k5cse34cy.png)
![x=\frac{-10\pm\sqrt[]{36}}{8}](https://img.qammunity.org/2023/formulas/mathematics/college/zfvrk705eexrxk272qjdrrov2uvkw64zcj.png)
the values of x are
x=-1/2 and x=-2
therefore
(4x^2+10x+4)=4(x+1/2)(x+2)=(4x+2)(x+2)
and the answer is
x(x-1)(4x+2)(x+2)=0