First let's fill the things we know from the table:
G=6.67e-11 m3/kgs2
M=1.99e30 kg
r=7.33e11 m
Now, to find the acceleration of the asteroid we use:
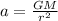
Plugging the values we know we have that the acceleration of the asteroid is:
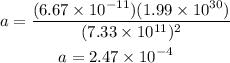
Therefore the acceleration is 2.47e-4 m/s2.
The velocity is given by:
![v=\sqrt[]{ar}](https://img.qammunity.org/2023/formulas/physics/college/wjg08t29vz2hubv2hxfyumcanlzei5s62v.png)
then we have:
![\begin{gathered} v=\sqrt[]{(2.47*10^(-4))(7.33*10^(11))} \\ v=1.35*10^4 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/y3s90s4cd7gienvl707ok3pgwubmbmshhu.png)
Therefore the velocity is 1.35e4 m/s
Finally the period is given as:
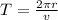
then:

Therefore the period is 3.41e8 seconds. Now, this is the same as 10.8 years; to get this we divide the seconds by 3.154e7