Answer:
0.09 = 9% probability that the student is proficient in neither reading nor mathematics
Explanation:
We solve this question treating the events as Venn probabilities.
I am going to say that:
Event A: A student is proficient in reading.
Event B: A student is proficient in mathematics.
A total of 82% of the students were found to be proficient in reading
This means that
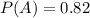
74% were found to be proficient in mathematics
This means that
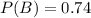
65% were found to be proficient in both reading and mathematics.
This means that
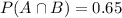
What is the probability that the student is proficient in neither reading nor mathematics?
This is:
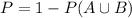
In which
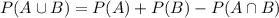
With the values that we have:
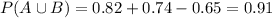
Then
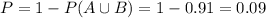
0.09 = 9% probability that the student is proficient in neither reading nor mathematics