Question

Can someone help me with this geometry question?The first box has four options: cylinder, square pyramid, cone, triangular prism

Answer 1

The shell is best modeled by a cone.

`SA=32\pi=100.6\text{ square inches}`

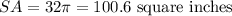
By the given choices, since the surface area is not a perfect cone, it has a small alteration at the bottom which increases the area. The approximate surface area of the shell is 107.4 square inches.

Explanation:

The seashell is best represented by a cone. The surface area of a cone is represented by the following equation:

`\begin{gathered} SA=\pi rs+\pi\cdot r^2 \\ \text{where,} \\ \\ r=\text{radius} \\ s=\text{ slant height} \end{gathered}`

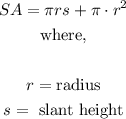
Then, use the Pythagorean theorem to find the slant height:

`\begin{gathered} s=\sqrt[]{2.5^2+10^2} \\ s=\frac{5\sqrt[]{17}}{2} \end{gathered}`

Now, solve for the surface area. If s=10.3, r=2.5

`\begin{gathered} SA=\pi\cdot2.5\cdot\frac{5\sqrt[]{17}}{2}+\pi\cdot(2.5)^2 \\ SA=25.75\pi+6.25\pi \\ SA=32\pi=100.6\text{ square inches} \end{gathered}`

By the given choices, since the surface area is not a perfect cone, it has a small alteration at the bottom which increases the area. The approximate surface area of the shell is 107.4 square inches.