Question

A quality control expert at life batteries wants to test their new batteries. The design engineer claims they have a variance of 8464 with the mean life of 886 minutes. If the claim is true in a sample of 145 batteries what is the probability that the main battery life will be greater than 904.8 minutes? Round answer to four decimal places

Answer 1

The parameters provided from the question is:

`\begin{gathered} \mu=886 \\ \sigma=√(8464)=92 \\ \bar{x}=904.8 \\ n=145 \end{gathered}`

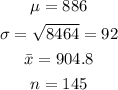
Using the z-score formula:

`z=\frac{\bar{x}-\mu}{(\sigma)/(√(n))}`

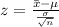
Substitute for the values provided and solve for z

`\begin{gathered} z=(904.8-886)/((92)/(√(145))) \\ z=2.4607 \end{gathered}`

The probability that the main battery life will be greater than 904.8 is given:

`\begin{gathered} P(z>2.4607)=P(0\leq z)-P(02.4607)=0.5-0.4931 \end{gathered}`
`P(z>2.4607)=0.0069`

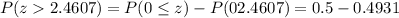
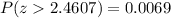
Hence, the probability that the main battery life will be greater than 904.8 is 0.0069