Question

Given: points A(5, 1), B(5,5), C(1,3), Q(-6,-5) and R(-4,-5). What coordinates for S would prove AABC~AQRS (T.G.7)(2 point) B с QR O A. (-4,-3) O B. (-5,-8) O C. (-3,-5) o D. (-5,-3)

Answer 1

Given:

A(5, 1), B(5, 5), C(1, 3)

Q(-6, 5), R(-4, -5), S(__, __)

To find the coordinates of S that would prove that ABC is similar to QRS, we have:

First Find the distance betweem AB and the distance between QR using the distance formula below:

`\begin{gathered} D=\sqrt[]{(x2-x1)^2+(y2-y1)^2} \\ \end{gathered}`

Distance between AB:

`\begin{gathered} AB=\sqrt[]{(5-5)^2+(5-1)^2} \\ \\ AB=\sqrt[]{0+16} \\ \\ AB\text{ = 4} \end{gathered}`

Distance between QR:

`\begin{gathered} QR=\sqrt[]{(-4--6)^2+(-5-}-5)^2 \\ \\ QR=\sqrt[]{(-4+6)^2+(-5+5)^2} \\ \\ QR\text{ = }\sqrt[]{(2)^2+(0)^2} \\ \\ QR=\sqrt[]{4} \\ \\ QR\text{ = 2} \end{gathered}`

Since ABC is similar to QRS, we have:

AB ~ QR

AB = 4

QR = 2

The scale factor is:

`(AB)/(QR)=(4)/(2)=2`

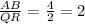
Since the scale factor is 2, Let's find the coordinates of S:

Find the distance between BC and AC .

Thus, we have:

The coordinates of S that would prove that ABC is similar to QRS is:

(-3, -5)

Choice C is correct

ANSWER:

C. (-3 -5)