Question

The distance that a spring will stretch varies directly as the force applied to the spring. A force of 80 pounds is needed to stretch a spring 8 inches. what force is required to stretch the spring 18 inches?

Answer 1

The equation that describes the stretching of springs is:

`F=k\cdot\Delta x\text{.}`

Where F is the force applied to stretch the spring a length Δx and k is the constant of the spring.

In this case, we have:

`\begin{gathered} F_1=80pd,\text{ }\Delta x_1=8in, \\ F_2=?,\text{ }\Delta x_2=18in\text{.} \end{gathered}`

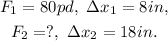
Replacing the values of F_1 and Δx_1 in the equation above, we have:

`\begin{gathered} F_1=k\cdot\Delta x_1, \\ 80pd=k\cdot8in\text{.} \end{gathered}`

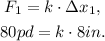
Solving for k, we get:

`k=(80pd)/(8in)=10(pd)/(in).`

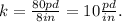
Replacing the value of k and Δx_2 in the equation, we get the value of F_2:

`F_2=k\cdot\Delta x_2=10(pd)/(in)\cdot18in=180pd\text{.}`

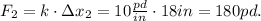
Answer

The force required to stretch the spring 18 in is 180 pounds.