The given functions are
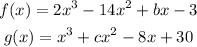
Since f(x) has a zero x = 2, then
Substitute x by 2 and equate the answer by 0 to find b
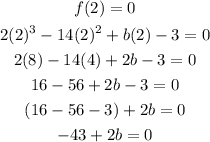
Add 43 to both sides
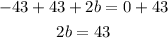
Divide both sides by 2
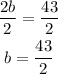
Then, f(x) is
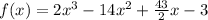
We will do the same with g(x)
Since g(x) has a root x = 3 - i, then there is another root x = 3 + i
Then substitute x by 3 - i and equate the answer by 0
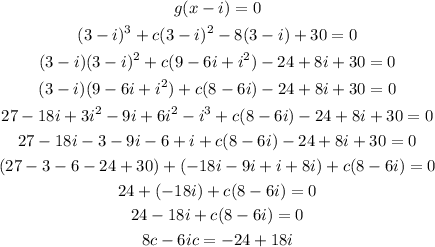
By comparing the 2 sides, then
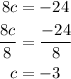
Then g(x) is
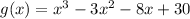
Now, multiply f and g, then substitute x by -1
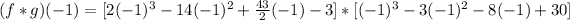
Simplify each bracket
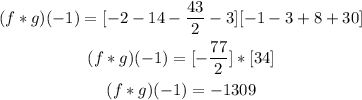
The answer is -1309