Question

Write a quadratic equation that has two solutions,0 and -2. Leave the polynomial in the equation infactored form.

Answer 1

Hello!

We can use the formula below to write a quadratic equation in the factored form, as we know the roots of it:

`(x-(x_1))\cdot(x-(x_2))=0`

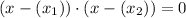
Let me explain it:

We will invert the signal of each root and sum it to x. Then, we will multiply the terms.

Let's replace with the values:

`\begin{gathered} (x-(0_{}))\cdot(x-(-2_{}))=0 \\ (x-0)\cdot(x+2)=0 \\ (x)\cdot(x+2)=0 \end{gathered}`

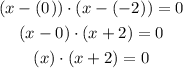
So, the equation in the factored form is (x) * (x+2) = 0.