Question

7)Basketball TournamentSchoolAppearancesUNC Greensboro2Appalachian State2Houston Baptist1Prairie View A&M1Alabama State4School AppearancesComell5Richmond9Eastern Illinois2lowa24Villanova34School AppearancesEvansville5Ball State7Southem8Northeastern8Cal State LA1A)B)48 12 16 20 24 28 324 812 16 20 24 28 32C)D)4 8 12 16 20 24 28 324 812 16 20 24 28 32

Answer 1

To draw the box plot the corresponds to the sample shown on the table, you have to determine the minimum and maximum values of the sample and the first, second, and third quartiles. To determine these values, you have to order the sample from least to greatest:

1, 1, 1, 2, 2, 2, 4, 5, 5, 7, 8, 8, 9, 24, 34

The sample corresponds to the appearances of 15 schools on the tournament, so n=15

The first quartile (Q₁)

To determine the position of the first quartile, given that the sample is odd, you have to use the following formula:

`\text{PosQ}_1=(1)/(4)(n+1)`

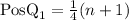
For n=15

`\begin{gathered} \text{PosQ}_1=(1)/(4)(15+1) \\ \text{PosQ}_1=(1)/(4)\cdot16 \\ \text{PosQ}_1=4 \end{gathered}`

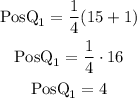
The first quartile corresponds to the fourth observation

1, 1, 1, 2, 2, 2, 4, 5, 5, 7, 8, 8, 9, 24, 34

The first quartile is Q₁=2

The second quartile (Q₂)

To determine the position of the second quartile, given that the sample is odd, you have to use the following formula:

`\text{PosQ}_2=(1)/(2)(n+1)`

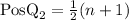
For n=15

`\begin{gathered} \text{PosQ}_2=(1)/(2)(15+1) \\ \text{PosQ}_2=(1)/(2)\cdot16 \\ \text{PosQ}_2=8 \end{gathered}`

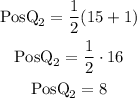
The second quartile corresponds to the eighth observation.

1, 1, 1, 2, 2, 2, 4, 5, 5, 7, 8, 8, 9, 24, 34

The second quartile is Q₂=5

The third quartile (Q₃)

To determine the position of the third quartile you have to use the following formula:

`\text{PosQ}_3=(3)/(4)(n+1)`

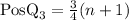
For n=15

`\begin{gathered} \text{PosQ}_3=(3)/(4)(15+1) \\ \text{PosQ}_3=(3)/(4)\cdot16 \\ \text{PosQ}_3=12 \end{gathered}`

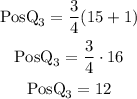
The third quartile corresponds to the twelfth observation of the sample:

1, 1, 1, 2, 2, 2, 4, 5, 5, 7, 8, 8, 9, 24, 34

The third quartile is Q₃=8

Now that we know the values that determine the "box", which are the first and third quartiles, we can proceed to determine the whiskers.

Note that the observations of the sample are quite close, except for the last two observations "24" and "34". These two observations can be outliers, so before we can determine the length of the whiskers of the sample, we have to determine the limit where observation can be considered an outlier.

Considering the first (Q₁) and third (Q₃) quartiles and the interquartile range (IQR), any value of the data set "X" can be considered an outlier if:

X < Q₁ - 1.5 IQR

X > Q₃ + 1.5IQR

The interquartile range is the difference between the third and first quartiles:

`\text{IQR}=Q_3-Q_1`

For Q₁=2 and Q₃=8

`\begin{gathered} \text{IQR}=8-2 \\ \text{IQR}=6 \end{gathered}`

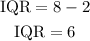
You can determine the limit, in which any value of the sample can be considered an outlier as follows:

Outliers to the left:

Outliers to the right:

[tex]\begin{gathered} X>Q_3+1.5\text{IQR} \\ X>8+1.5\cdot6 \\ X>8+9 \\ X>17 \end{gathered}" src="

→ Any observation above 17 can be considered an outlier. For our sample, we have two right outliers, 24 and 34.

Once we have determined the presence of outliers, we can determine the length of the whiskers, to do so, you have to consider the sample without the outliers:

1, 1, 1, 2, 2, 2, 4, 5, 5, 7, 8, 8, 9

The minimum value is 1 and the maximum value is 9.

Box limits are defined by Q₁=2 and Q₃=8, the line inside the box represents the second quartile Q₂=5.

Whiskers: The left whisker goes from the minimum value 1 to the first quartile 2.

The right whisker goes from the third quartile 8 to the maximum value 9.

There are two positive outliers 24 and 34

You can draw the box plot as follows:

The correct box plot is option C