Given the following expression:
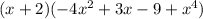
Let's simplify;
Applying the PEMDAS Rule (Parenthesis, Exponent, Multiplication, Division, Addition and Subtraction).
Step 1: Simplify first the equation within the parenthesis.
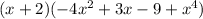
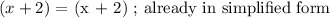
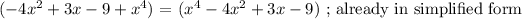
Step 2: Proceed with the multiplication.
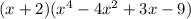
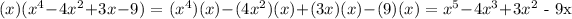
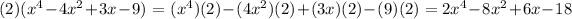
Step 3: Let's add the product of x and 2 being multiplied to -4x^2+3x-9+x^4.
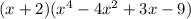
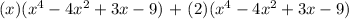
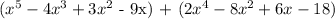
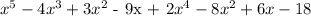
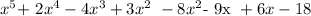
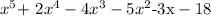
Therefore, the product of (x+2) (-4x^2+3x-9+x^4) is x^5 + 2x^4 -4x^3 -5x^2 -3x - 18.