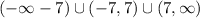Step-by-step explanation
Given
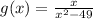
The domain of the function is the set of x values that will make the function defined. This is given below.
Using the denominator, we will find the point of singularity.
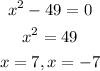
Therefore, the points of singularities are 7 and -7. Hence we will exclude those points from the set of real numbers.
Answer: