Question

Suppose that the distribution for a random variable x is normal with mean 9 and standard deviation σ, and P(x<0)=0.0658. Rounded to two decimal places, what is σ?

Answer 1

Given:

mean = 9

x = 0

probability of x < 0 = 0.0658

Find: standard deviation

Solution:

To find the value of the standard deviation, here are the steps.

1. Using the standard normal distribution table, find the z-value that covers an area of 0.0658 on its left.

Normally, the standard normal distribution table shows areas starting from the center of the mean. So, let's subtract 0.0658 from 0.5 first.

`0.5-0.0658=0.4342`

Let's use the probability 0.4342. Let's find the z-value that has an area of 0.4342 from the center of the mean.

Based on the normal distribution table, the z-value that has an area of 0.4342 from the center of the mean is z = -1.508.

2. Now that we have the z-value = -1.508, let's use the formula below to identify the standard deviation.

`\sigma=(x-\mu)/(z)`

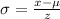
Let's plug in the given information to the formula above including the calculated z.

`\sigma=(0-9)/(-1.508)`

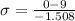
Then, solve.

`\sigma=(-9)/(-1.508)\Rightarrow\sigma=5.9682\approx5.97`

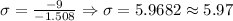
Therefore, the value of the standard deviation is 5.97.