SOLUTION
The slope-intercept form for the equation of a line is given by
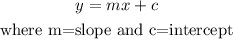
Giving the point

Then
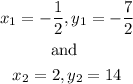
We apply the two point-form for the equation of a line
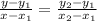
Substituting the values into the formula, we obtain
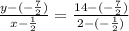
Simplify the equation above
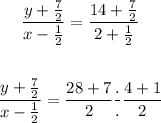
Then, change the division to multiplication and take the reciprocal of the last fraction
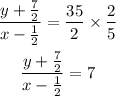
Multiply both parts of the equation by the denominator (x-1/2), we obtain
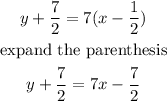
Then, make y the subject of the formula
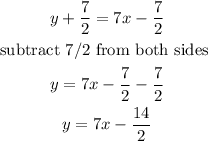
Hence the equation of the line becomes
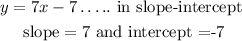
Therefore the equation of the line in slope-intercept is
y=7x-7