The position function of a particle is given by:
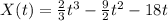
The velocity function is the derivative of the position:
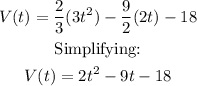
The particle will be at rest when the velocity is 0, thus we solve the equation:

The coefficients of this equation are: a = 2, b = -9, c = -18
Solve by using the formula:
![t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/3cgw61gskglny4a505tle5b9wokluktv58.png)
Substituting:
![\begin{gathered} t=\frac{9\pm\sqrt[]{81-4(2)(-18)}}{2(2)} \\ t=\frac{9\pm\sqrt[]{81+144}}{4} \\ t=\frac{9\pm\sqrt[]{225}}{4} \\ t=(9\pm15)/(4) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jm84vvpnpeoxs5v1wwbdptovanbdltfk09.png)
We have two possible answers:
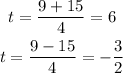
We only accept the positive answer because the time cannot be negative.
Now calculate the position for t = 6:
![undefined]()