Question

tan (θ) cot (θ)=1Trig: use trigonometric identities to transform the left side of the equation into the right side

Answer 1

1) Let's prove this identity

Since tan (θ) = sin(θ)/cos((θ)

And cot((θ) = cos ((θ)/sin((θ)

2) Let's plug it into:

`\begin{gathered} \tan \text{ (}\theta)\cot \text{ (}\theta)\text{ =1} \\ (\sin (\theta))/(\cos (\theta))\cdot(\cos (\theta))/(\sin (\theta))=1 \\ 1=1 \end{gathered}`

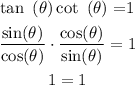
Simplifying (dividing) sin(θ) on the numerator, with sin (θ) on the denominator and similarly cos (θ) with cos(θ) we'll get to 1 over 1 time 1 over 1 = 1

Then 1=1