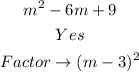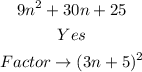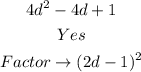Question

I need help with this question. Determine if each trinomial is a perfect square trinomial. Write yes or no if yes factor it.

Answer 1

Perfect square trinomials are algebraic expressions with three terms that are obtained by multiplying a binomial with the same binomial.

To determine if the trinomials in the question is a perfect trinomial, we will factor each of the trinomials and then decide which is a perfect trinomial

`\begin{gathered} m^2-6m+9 \\ \rightarrow m^2-3m-3m+9 \\ \rightarrow m(m-3)-3(m-3) \\ \rightarrow(m-3)(m-3) \\ \rightarrow(m-3)^2 \end{gathered}`

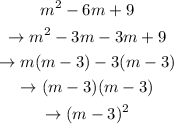
The first trinomial above is a perfect trinomial

`\begin{gathered} 9n^2+30n+25 \\ \rightarrow9n^2+15n+15n+25 \\ \rightarrow3n(3n+5)+5(3n+5) \\ \rightarrow(3n+5)(3n+5) \\ \rightarrow(3n+5)^2 \end{gathered}`

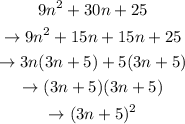
The second trinomial above is a perfect trinomial

`\begin{gathered} 2w^2-4w+9 \\ can\text{ not be farctored} \end{gathered}`

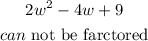
The third trinomial above is not a perfect trinomial

`\begin{gathered} 4d^2-4d+1 \\ \rightarrow4d^2-2d-2d+1 \\ \rightarrow2d(2d-1)-1(2d-1) \\ \rightarrow(2d-1)^2 \end{gathered}`

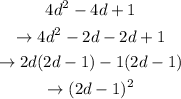
The fourth trinomial above is a perfect trinomial

The summary of the solution is given below

`\begin{gathered} m^(2)-6m+9 \\ Yes \\ Factor\rightarrow(m-3)^2 \end{gathered}`

`\begin{gathered} 9n^(2)+30n+25 \\ Yes \\ Factor\rightarrow(3n+5)^2 \end{gathered}`
`\begin{gathered} 2w^(2)-4w+9 \\ No \\ Factor\rightarrow none \end{gathered}`
`\begin{gathered} 4d^2-4d+1 \\ Yes \\ Factor\rightarrow(2d-1)^2 \end{gathered}`