We must mix 4 gallons of a 90% alcohol solution and 8 gallons of a 30% alcohol solution.
We can solve the exercise writing two equations. In these equations let's call x the 30% alcohol solution and y the 90% alcohol solution:
- equation 1: x.(0.3) + y.(0.9) = 12.(0.5)
- equation 2: x+y=12
Now, we can replace x from the equation 2 on equation 1.
First, from equation 2 we resolve x=12-y so we can replace it on the equation 2:
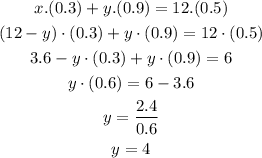
So, it is needed 4 gallons of 90% alcohol solution.
Finally, we replace the value of y=4 on the equation 2 to find x:
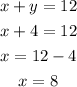
And It is needed 8 gallons of 30% alcohol solution.
We must mix 4 gallons of a 90% alcohol solution and 8 gallons of a 30% alcohol solution.