Since the equation of the curve is
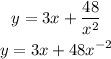
The slope of the tangent of the curve at the point (x, y) is y'
The normal and the tangent are perpendicular at this point
Then we will find the slope of the tangent, then find from it the slope of the normal
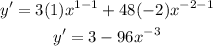
Since we need the tangent at x = 4, then substitute x by 4 in y'
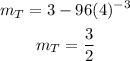
To find the slope of the normal, reciprocal the m and change its sign
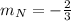
The form of the equation is y = mx + b, where m is the slope and b is the y-intercept
The equation of the normal is
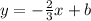
To find b we need a point on the curve
Since x = 4, substitute it in the equation of the curve to find its corresponding y
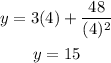
Then substitute x and y in the equation of the normal by 4 and 15
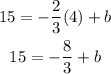
Add -8/3 to both sides
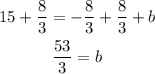
The equation of the normal is
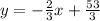
Multiply all terms by 3 to cancel the denominators
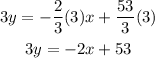
Add 2x to both sides
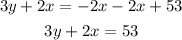
Subtract 53 from both sides
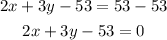
The equation of the normal is 2x + 3y - 53 = 0