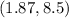The equation for the distance between any point and the point (0, 9) is:

The curve given in the problem is:
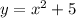
If we solve for 'x²', we can substitute in the distance equation and obtain a function for the distance of any point in the curve to (0, 9):

And substitute:
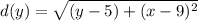
SImplify:
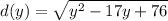
And now, we need to calculate the first and second derivatives:
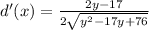
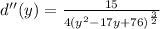
Then, find the critical points of d(y). Since this function is a quotient, it will be equal to 0 when the numerator is equal to 0:
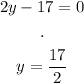
Now, evaluate this value into the second derivative:
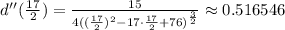
Since is a positive value, the function d(y) has a minimum in y = 17/2
Next, we need to find the values of x. We use the equation of the curve:
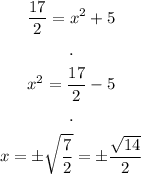
Thus, the point on the curve closest to (0, 9), rounded to two decimals, are: