We have an expression for the velocity of the particle:
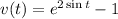
We have to find when the particle moves to the left.
As the particle moves along the x-axis, this means that the velocity is negative.
We then have to find the interval where v(t) < 0.
We can find this interval as:
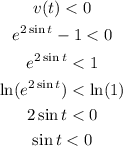
The function sin(t) is negative for intervals between π and 2π per cycle.
As t is defined from 0 to 16, we can calculate how many cycles we have:
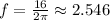
We will have at least 2 intervals or 3 at most where sin(t) < 0.
We can list the intervals as:
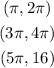
The third period is cut at t = 16.
We can skecth the velocity as:
We can round the intervals to the nearest thousand as:

Answer: the intervals for t are (3.142, 6.286), (9.425, 12.566) and (15.708, 16).