1 Answer

Ask a Question

Roemer · Answer 1 · 2023-02-26T22:14:50+0000

We are going to divide in three parts to find the volume, so the first parte is the rigth one where we have the last step.

$\begin{gathered} V_1=(45\operatorname{cm})\cdot(100\operatorname{cm})\cdot(100\operatorname{cm}) \\ =450000cm^3=4500m^3 \end{gathered}$

Because we have to take acount the base of the steps not just the steps, now for the second step we have

$\begin{gathered} V_2=(30\operatorname{cm})\cdot(100\operatorname{cm})\cdot(25\operatorname{cm}) \\ =75000cm^3=750m^3 \end{gathered}$

$\begin{gathered} V_2=(30\operatorname{cm})\cdot(100\operatorname{cm})\cdot(25\operatorname{cm}) \\ =75000cm^3=750m^3 \end{gathered}$
$\begin{gathered} V_3=(15\operatorname{cm})\cdot(100\operatorname{cm})(25\operatorname{cm}) \\ =37500cm^3=375m^3 \end{gathered}$

So the total volume is

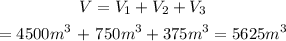
$\begin{gathered} V=V_1+V_2+V_3 \\ =4500m^3\text{ + }750m^3+375m^3=5625m^3 \end{gathered}$

The answer is 5625 m3.

And for the fist step we have

$\begin{gathered} V_3=(15\operatorname{cm})\cdot(100\operatorname{cm})(25\operatorname{cm}) \\ =37500cm^3=375m^3 \end{gathered}$

So the total volume is

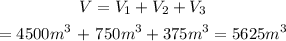
$\begin{gathered} V=V_1+V_2+V_3 \\ =4500m^3\text{ + }750m^3+375m^3=5625m^3 \end{gathered}$

The answer is 5625 m3.

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions