Question

A sailboat runs before the wind with a constant speed of 3.2m/s2 in a direction 42 degree north of west. How far (a) west and (b) north has the sailboat traveled in 25min?

Answer 1

Given:

Speed = 3.2 m/s²

Direction, θ = 42 degrees north of west.

Let's solve for the following:

(a) How far west has the sailboat traveled in 25 minutes.

We have the free body diagram below:

To find the distance, let's first find the x-component and y-component of the velocity.

x-component:

`\begin{gathered} Vx=-V\cos \theta \\ V_x=-3.2\cos 42 \\ V_x=-2.378\text{ m/s} \end{gathered}`

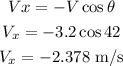
y-component:

`\begin{gathered} V_y=V\sin \theta \\ V_y=3.2\sin 42 \\ V_y=2.141\text{ m/s} \end{gathered}`

To find the distance travelled west, we are to find the distance in the x direction.

Apply the formula:

`d=|V_x|t`

Where:

|Vx| = |-2.378 m/s| = 2.378 m/s

t is the time is seconds = 25 x 60 = 1500 seconds

Thus, we have:

`\begin{gathered} d=2.378\ast1500 \\ \\ d=3567.1\text{ m }\approx\text{ 3.6 km} \end{gathered}`

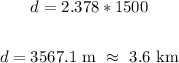
The distance traveled west in 25 minutes is 3.6 km.

• (b) How far north has the sailboat traveled in 25 minutes.

Here, we are to find the vertical distance using the y-component.

Apply the formula:

`d=|V_y|t`

Where:

Vy = 2.141 m/s

t = 1500 seconds

Thus, we have:

`\begin{gathered} d=2.141\ast1500 \\ \\ d=3211.5\text{ m }\approx3.2\text{ km} \end{gathered}`

The sailboat traveled 3.2 km in the north direction.

ANSWER:

(a) 3.6 km

(b) 3.2 km