Question

In the figure below, quadrilateral RATS is a rhombus with diagonals SA and TR interesting at E.

Answer 1

We need to find the length of the sides SR, RT, and the angle m∠TAS.

Finding the length of SR:

We consider that, in a rhombus, all of the sides are equal. So the sides ST and SR have to be equal:

`ST=SR`

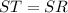
Substituting the values of these sides:

`3x+30=8x-5`

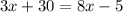
We need to solve this equation for x.

Subtract 3x to both sides:

`\begin{gathered} 30=8x-3x-5 \\ 30=5x-5 \end{gathered}`

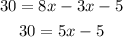
Add 5 to both sides:

`\begin{gathered} 30+5=5x \\ 35=5x \end{gathered}`

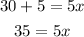
Divide both sides by 5:

`\begin{gathered} (35)/(5)=x \\ 7=x \end{gathered}`

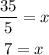
Now that we have the value of x, we can find the value of SR:

`\begin{gathered} SR=8x-5 \\ \text{substituting x=7} \\ SR=8(7)-5 \\ \text{Solving the operations:} \\ SR=56-5 \\ SR=51 \end{gathered}`

SR=51

Finding the length of RT:

To find this length we need the value of z. And we can find the value of z considering that the diagonals bisect each other, so each side of a diagonal is equal to the other side of the diagonal. In this case, the blue and the red line in the image are equal:

We have that:

`SE=AE`

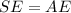
Substituting the values of SE and AE:

`3z=4z-8`

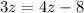
And now we solve for z by subtracting 3z to both sides:

`\begin{gathered} 0=4x-3z-8 \\ 0=z-8 \\ \text{Add 8 to both sides:} \\ 8=z \end{gathered}`

With this value of z, we can find the length RT.

RT is the yellow line in the image:

Again we consider that the two sides of the diagonal are equal. Thus, RT is equal to:

`\begin{gathered} RT=5z+5+5z+5 \\ \text{Combining like terms:} \\ RT=10z+10 \\ \text{substituting z=8} \\ RT=10(8)+10 \\ RT=80+10 \\ RT=90 \end{gathered}`

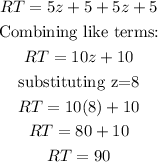
RT=90

Finally, we need to find the angle m∠TAS shown in blue in the image:

Since it is a rhombus, all of the angles in point E are equal to 90°:

So, considering only the triangle inside the rhombus marked in blue

We apply the property of triangles that tells us:

The sum of the internal angles of a triangle is equal to 180°.

So adding all of the blue angles we should get 180:

`90+9y+8+5y-2=180`

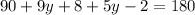
And now we solve for y, first, combine like terms:

`96+14y=180`

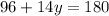
Subtract 96 to both sides:

`\begin{gathered} 14y=180-96 \\ 14y=84 \end{gathered}`

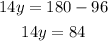
Divide both sides by 14:

`\begin{gathered} y=(84)/(14) \\ y=6 \end{gathered}`

And now that we have the value of y, we can find the value of m∠TAS:

`\begin{gathered} m\angle TAS=9y+8 \\ \text{Substituting y=6} \\ m\angle\text{TAS}=9(6)+8 \\ m\angle TAS=54+8 \\ m\angle TAS=62 \end{gathered}`

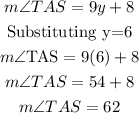
m∠TAS=62°

Answer:

SR=51

RT=90

m∠TAS=62°