In order to solve this question it's useful to remember that the sum of the internal angles of a triangle is equal to 180°.
Firstly, let's take a look at the angles which have D as their vertex. These two angles are BDC and BDA and they both share a side whereas their remaining sides are in the same line. This means that these two are supplementary which means that their sum is equal to 180°. Knowing that the measure of BDC is equal to 90° we get:

If we substract 90° from both sides:
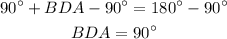
So both angles are right angles.
Having found the measure of angle BDA let's take a look at triangle BDA. We have a 45° angle, a 90° angle and angle b. Since the sum of these 3 must be equal to 180° so we get:
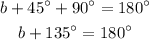
Then we substract 135° from both sides:
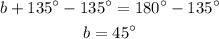
So we have found b. We still need to find a. Let's take a look at vertex B. The external angle is equal to 275° whereas there are two internal angles: a 45° angle and angle DBC. The sum of the external and internal angles in a vertex must be equal to 360° then we have:

If we substract 320° from both sides we get:
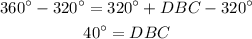
Now that we have angle DBC we can find angle a by looking at triangle BDC. The sum of its internal angles is 180° and we already know two of them: DBC and BDC. Then we get:
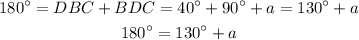
Then if we substract 130° from both sides we get:
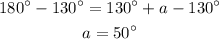
So now we know that a=50° and b=45°. Then a is bigger than b by 5° and the answer is option c.