In the equation of the parabola, the value for p represents the distance between the vertex and the focus. To find it, use the formula to find the distance between 2 points:
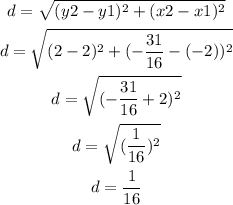
It means that the value of p is 1/16, in decimal form, 0.0625.
The value of h is the x coordinate of the vertex, which is -2.
The value of k is the y coordinate of the vertex, which is 2.