Question

Can you please help me with my questions 6 on my home work

Answer 1

Identify the coordinate of each point

`\begin{gathered} x=(-1,2) \\ y=(2,6) \\ \text{and } \\ z=(9,2) \end{gathered}`

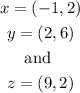
Find the distance each point which represent the length of the sides

Using the formula for distance between two point

`\begin{gathered} |xy|=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{where } \\ x_2=2,x_1=-1,y_2=6,y_1=2 \\ \text{Hence} \\ |xy|=\sqrt[]{(2-(-1)^2+(6-2)^2} \\ |xy|=\sqrt[]{3^2+4^2} \\ |xy|=\sqrt[]{9+16}=\sqrt[]{25} \\ |xy|=5\text{ unit} \end{gathered}`

The lenght of |XY|= 5 unit

Similarly, we find the side length of |YZ|, using the same approach

`\begin{gathered} |YZ|=\sqrt[]{(9-2)^2+(2-6)^2} \\ |YZ|=\sqrt[]{7^2+(-4)^2} \\ |YZ|=\sqrt[]{49+16} \\ |YZ|=\sqrt[]{65}\text{ unit} \end{gathered}`

The lenght of |YZ| is 8.06 unit

We now obtain the length of the side |XZ|

`\begin{gathered} |XZ|=\sqrt[]{(9-(-1)^2+(2-2)^2} \\ |XZ|=\sqrt[]{10^2^{}+0^2} \\ |XZ|=\sqrt[]{100}=10\text{ unit } \end{gathered}`

The lenth of |XZ| is 10 unit

The Area of of triangle with three sides is given by

Applying the formula above, we have

`\begin{gathered} \text{Area of triangle }\Delta XYZ\text{ is } \\ s=(5+10+8.06)/(2)=23.06\text{ square unit } \\ Then \\ \text{Area}=\sqrt[]{23.06(23.06-5)(23.06-10)(23.06-8.06)} \\ \text{Area}=285.63\text{ square unit } \end{gathered}`

Since the sides are not equal, XYZ is a scalence Triangle , |XY| is 5 unit, are the right options

See the image below