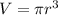We will have the following:
First, we can see that the volume of the sphere and the regular cone are given by:
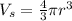
And:
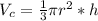
Now, since the volume of the cone is inscribed by a maximum stablished by the sphere, we know that the maximum height for the cone will be equal to the radius of the sphere, so, we re-write the volume of the cone:
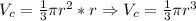
i. Now, we determine the ratio of both volumes as follows:
[Cone to sphere]
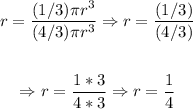
So, the ratio of the volumes of the cone to the sphere will be of 1:4.
ii. And the expression in terms of r for the volume inside the sphere but outside the cone will be:
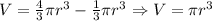
So, the expression is: